SuiveurLigne2012-1 : Différence entre versions

Version du 23 mai 2013 à 15:05

Introduction

/* Attentions aux coquilles et autres fautes d'orthographe et de grammaire */

A travers cette page, je vais vous présenter les étapes successives de mon travail dans le cadre des bureaux d’études PEIP. Premièrement, l’objectif sera de réaliser un robot en Lego MindStorm capable de suivre un marquage continu ou non. C’est le robot suiveur de ligne.

Toutefois, il existe de multiples procédés pour parvenir à un tel objectif. Afin de les limiter, le robot doit respecter divers directives que voici :

(1) en cas de perte du marquage, tourner dans un sens puis dans l'autre pour tenter de le retrouver avec des angles de plus en plus grands.

(2) si le marquage ne peut pas être retrouvé, se remettre dans la position de la perte initiale et partir tout droit.

(3) se remettre dans l'axe du marquage lorsque ce marquage est retrouvé.

(4) s'arrêter quand un obstacle se présente devant lui et repartir si l'obstacle disparait.

(5) changer de parcours sur commande, c'est à dire emprunter un parcours d'une couleur différente dès qu'il est rencontré.

(6) inverser son sens de parcours.

Les premiers pas …

… de la construction

Avant tout, j'ai monté le robot. La base de la structure a été réalisée avec le modèle de construction du manuel Lego; intégrant 3 moteurs et un boîtier NXT.

• 

  La base motrice

Enfin, pour que le robot ait des informations sur son environnement il est nécessaire d’y rajouter des capteurs. Pour débuter, seul deux capteurs m’ont paru les plus appropriés : le capteur de couleurs particulièrement utile pour suivre un marquage et le capteur à ultrasons pour détecter les obstacles (directive n°4).

• 

  Le capteur à ultrasons

• 

  Le capteur de couleurs

• 

  Le capteur de couleurs en fonctionnement

Du travail est encore à faire concernant le montage du robot, l’emplacement pour la Fox Board est prévu mais celle-ci n’est pas encore parfaitement stable. Concernant les capteurs, il sera surement utile d’en rajouter d’autres. En outre, la base de la structure comprend 3 moteurs hors seul deux suffiraient. Et à l’usage, j’ai constaté qu’il n’était pas aisé de changer les piles du boîtier NXT.

… de la programmation

Une fois les deux capteurs et le boîtier NXT mis en place, j’ai tenté de faire rouler le robot avec le logiciel Lego MindStorm. Les premiers essais ont été concluants puisque j’ai réussi à mettre en mouvement le robot dans différentes directions et à faire fonctionner les capteurs. Cependant le logiciel ne me semblait pas facile à manipuler pour faire des programmes plus compliqués avec plusieurs boucles notamment. J’ai donc essayé avec le logiciel Bricx Command Center où il est possible de coder avec un langage proche du C. Malheureusement, j’ai beaucoup de difficulté à trouver les fonctions du logiciel et je ne suis pas parvenue à faire fonctionner les capteurs. Finalement, j’en avais effectué plus avec le logiciel Lego MindStrom. Les séances de cours passant rapidement, je suis donc retourné sur ce logiciel. Malgré que je ne le maîtrise pas encore très bien, j’ai décidé de commencer mes programmes pour atteindre les objectifs en espérant apprendre plus efficacement.

Comment lui faire suivre un marquage continu ?

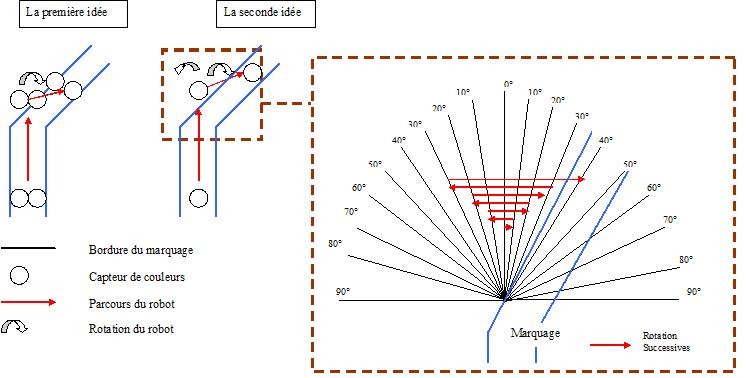
Dans un parcours à suivre, on peut évidemment distinguer les lignes droites, des virages. Dans les lignes droites ou les très légers virages le robot détecte toujours la couleur en continuant tout droit. Dés le premier virage, il va perdre le marquage. Pour le retrouver deux méthodes, me sont venues: la première qui est d’utiliser deux capteurs de couleurs un droit et un gauche. Dés que la couleur n’est plus détectée par l’un des capteurs il va falloir tourner d’un certain angle jusqu’à ce que le capteur qui avait perdu la ligne la perçoive de nouveau. Ceci impose un capteur supplémentaire et des contraintes importantes sur la largeur de la ligne à suivre. La deuxième idée est de lui faire retrouver le marquage qu’il a perdu en effectuant des rotations dans un sens puis dans l’autre. Celle-ci est préférable puisqu’elle peut servir pour les lignes discontinues.

Finalement, voici la première structure de mon programme pour un parcours dont le marquage est bleu :

 Tant que (infinie)
      {
       Si le capteur de couleurs détecte du bleu 
           Avancer tout droit ;
       Sinon faire la deuxième idée
      }

Il s’agit maintenant de programmer cette deuxième idée. Pour cela, il nous faut une boucle :

 Tant que le capteur de couleurs ne détecte pas de bleu 
    {
    Tourner d’un multiple d’un angle Alpha dans un sens et dans l’autre
    }

(Dans le schéma Alpha = 10°)

J’ai constaté que la rotation du robot était définie par un nombre K compris entre -100 et 100 dans le bloc moteur du logiciel Lego MindStorm. Si K est positif, il tourne dans le sens trigonométrique, négatif dans l’autre sens et |K| correspond à la valeur d’un angle.

J’ai d’abord pensé à faire l’algorithme ci-dessous :

 K < -  1 ;
 Tant que le capteur de couleurs ne détecte pas de bleu 
    { 
    Bloc moteur < -  f(K) ;
    K < -   K+1 ;
    }
Où f(K) = ((-1)^K) * (K) * Alpha

Le premier terme (-1)^K modifie le signe de la fonction à chaque incrémentation de K. Si K est pair (f(K) est positif), le robot va tourner dans le sens trigonométrique. Au contraire, si K est impair (f(K) est négatif), le robot va tourner dans l’autre sens. Le terme (K*Alpha) modifie l’amplitude de la rotation.

On a pour Alpha = 10° :

K: 	1	2	3	4
f(K):	-10°	20°	-30°	40°

Malheureusement, je suis très vite tombée dans les inconvénients du logiciel. Pour programmer l’incrémentation d’une variable K, il est nécessaire d’utiliser 5 blocs. Donc la programmation de f(K) serait trop lourde, notamment à cause de la puissance. Avec les conseils de nos chers professeurs, j’ai appris qu’il était mieux de faire un « Switch » qui prend en compte toutes les valeurs de K.

Voici l’algorithme :

 K < -  0 ;
   Tant que le capteur de couleurs ne détecte pas de bleu 
   { 
   K < -   K +1 ;
   Switch (K) :
      {
      Cas K=1  : Bloc moteur < -  (- Alpha) ;
      Cas K=2  : Bloc moteur < -  (2* Alpha) ;
      Cas K=3  : Bloc moteur < -  (-3* Alpha) ;
      .
      .
      .	          
      }
   }

Pour que le robot tourne par pas de 10°, Alpha doit être égal à 5,5. Cette valeur est obtenu par un simple produit en croix (200 * 10° / 360°).

 Tant que (infinie)	
   {
   Si le capteur de couleurs détecte du bleu 
      Avancer tout droit ;
   Sinon K < -  0 ;
   Tant que le capteur de couleur ne détecte pas de bleu 
      { 
      K < -   K +1 ;
      Switch (K) :
         {
         Cas K=1 : Bloc moteur < -  (- Alpha) ;
         Cas K=2  : Bloc moteur < -  (2* Alpha) ;
         Cas K=3  : Bloc moteur < -  (-3* Alpha) ;
         .
         .
         .	          
         }
         }
      }

Il sait suivre une ligne

Le robot suit maintenant correctement un marquage continu. Quand est-il pour les marquages discontinus et les directives (4), (5) et (6) ?

Comment lui faire suivre une ligne discontinue ?

Dans cette partie je vais aborder comment j’ai répondu aux directives (2) et (3).

Que faut-il faire ?

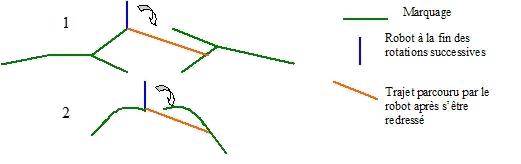
En cas d’interruption du marquage, après avoir effectué toutes ses rotations le robot doit se remettre dans l’axe du marquage et partir tout droit pour le retrouver plus loin. Il est très difficile de se remettre exactement dans l’axe. C’est pourquoi, il existe différents types de discontinuités qui n’empêchent pas le robot de retrouver le marquage bien que celui-ci ne soit pas parfaitement dans l’axe.

Voici ces discontinuités :

Une ligne discontinue

Je n’ai pas eu trop de difficulté à trouver l’algorithme pour que le robot interrompt les rotations successives et repart récupérer le marquage perdu plus loin.

Mon algorithme repose uniquement sur la détection de couleur et la rotation des roues. Le gros problème que j’aie rencontré concerne les rotations successives décrites dans la partie 3. En effet, pour un même nombre de rotation de la roue, la trajectoire des roues n’est pas la même. Le robot déviait sur la gauche.

Pour des angles de rotation faible, la déviation restait négligeable. Dans les lignes continues le robot n’avait pas besoin de balayer des angles de -90° à 90°, de -40° à 40° été suffisant. Je me suis seulement rendu compte de ce problème lorsque j’ai voulu abordé le suivi des lignes discontinues.

Enormément de temps a été consacré pour essayer d’éviter la déviation sur la gauche. Modification sur l’anatomie du robot, sur l’algorithme des rotations,… J’ai essayé différente forme de ligne, différent support … rien n’a fonctionné.

Bien que l’algorithme soit correct, la mécanique de mon robot ne permettait pas de régler de cette façon le problème. En effet, les chenilles n’étant pas les mêmes, et le centre de gravité pas centré je ne suis pas parvenu à supprimer cette déviation.

Je regrette avoir passé beaucoup de temps à essayer de rectifier ce problème. Finalement, je réduis fortement le nombre de rotations successives (grandeur max dans l’algorithme ci-dessous) pour que la déviation du robot ne m’empêche pas d’atteindre l’objectif.

Voici mon algorithme:

Tant que (infinie) 
  { Si I < max 
           Si le capteur de couleurs détecte du bleu 
     		 avancer tout droit ;
           Sinon 
                Tant que ( pas de bleu et I < max )
                     rotation successive ;
                      I <- I+1 ; }
   Sinon I <- 0 ;
          Se remettre dans l’axe ;
          Tant que (pas de bleu)
                     avancer tout droit ;
  }

Je me demande aujourd’hui : Pourquoi ne pas avoir triché sur l’algorithme pour rectifier la déviation, en ajoutant une rotation supplémentaire sur la droite ?

S'arrêter quand il y a un obstacle

… à suivre.